Введение
Линейная алгебра служит связующим звеном между теорией и практической реализацией концепций. Итак, важно иметь четкое представление о линейной алгебре, чтобы расширить знания об алгоритмах машинного обучения, которые включают в себя немного сложные концепции. Одной из таких тем, о которой вы должны узнать, является разложение матрицы по сингулярным значениям для уменьшения размерности.
SVD присутствует повсюду, особенно в науке о данных или при работе с уменьшением размерности. Но что это значит и как это работает?
В этом блоге мы ответим на все подобные вопросы и более подробно.
Что такое сингулярная декомпозиция (SVD)?
Разложение по сингулярным значениям в машинном обучении означает разложение матрицы на три матрицы. Оно обладает несколькими алгебраическими свойствами, а также теоретическими и геометрическими представлениями о линейных преобразованиях.
Когда мы узнаем о SVD матрицы, мы часто будем сталкиваться с термином ‘ранг матрицы’. Итак, сначала давайте познакомимся с концепцией ранга матрицы.
Ранг матрицы
Ранг матрицы означает максимальное количество линейно независимых векторов-столбцов или строк в матрице.
Если вектор ‘r’ не может быть выражен как линейная комбинация векторов r1 и r2, он линейно независим от r1 и r2.
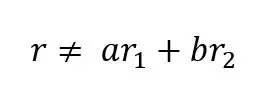
Взгляните на следующие три матрицы:

- В матрице A строка 2 (r2) кратна строке 1 (r1), т.е. r2= 2 r1. Таким образом, существует только одна независимая строка. Мы можем сказать, что ранг (A)= 1.
- Переходя к матрице B, строка 3 (r3) является суммой строк 2 и row1, т.е. r3= r1+ r2. Однако r1 и r2 независимы. Итак, ранг(B)= 2.
- В матрице C все заданные три строки независимы друг от друга. Итак, ранг(C)= 3.
Проще говоря, ранг матрицы отражает количество уникальной информации, представленной матрицей. Чем выше ранг, тем выше информация.
Сингулярная декомпозиция матрицы имеет дело с разложением матрицы на произведение 3 матриц:
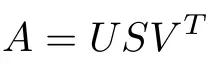
Допустим, размеры A равны m x n, тогда:
- U = m x m матрица левых сингулярных векторов.
- S = m x n прямоугольная диагональная матрица сингулярных значений, расположенных в порядке убывания.
- V = n x n матрица правых сингулярных векторов.
Почему SVD используется для уменьшения размерности?
Можно задаться вопросом, зачем проходить утомительную декомпозицию и брать на себя столько хлопот. Что ж, альтернативное представление декомпозиции поможет вам лучше понять причину.
Давайте взглянем на следующую диаграмму
С помощью декомпозиции мы можем выразить исходную матрицу как линейную комбинацию матриц низкого ранга.
Теперь, говоря о практическом применении, вы можете видеть, что только первые несколько особых значений (k) являются большими, в то время как остальные особые значения приближаются к нулю. Таким образом, мы можем игнорировать термины, за исключением первых нескольких, не упуская при этом большую часть информации.
Итак, мы можем сделать вывод:
- При разложении по сингулярным значениям мы можем представить большую матрицу A тремя меньшими матрицами, т.Е. U, S и V.
- Это очень удобно при больших вычислениях.
- Чтобы найти аппроксимацию A k-ранга, мы должны выбрать первые k сингулярных значений и соответствующим образом усечь три матрицы.
Приложения для разложения по сингулярным значениям
Общие области применения сингулярной декомпозиции заключаются в следующем:
- Он используется в науке о данных.
- Алгоритм SVD обладает некоторыми исключительными алгебраическими характеристиками и предлагает релевантную геометрическую и теоретическую информацию, связанную с линейным анализом.
- Он имеет большое применение в науке и технике.
- Он также используется в математике, например, для вычисления матричного приближения или ранга матрицы.
- Он также используется в статистике, такой как управление процессами и подгонка данных методом наименьших квадратов.
Прежде чем мы подробно обсудим приложения SVD, вот несколько ключевых моментов, которые следует знать:
- Ранг матрицы – это мера уникальной информации, хранящейся в матрице. Чем выше ранг, тем больше информации.
- SVD матрицы – это разложение матрицы на три матрицы.
- Собственные векторы матрицы относятся к направлениям максимального разброса или дисперсии данных.
- Сингулярные значения подобны важным значениям различных объектов в матрице.
SVD для сжатия изображений
Мы продолжаем нажимать на красивые картинки со своих смартфонов, и однажды мы понимаем, что у нас больше нет памяти или свободного места. Мы все проходили через эту ситуацию, не так ли? Следовательно, мы используем сжатие изображений, чтобы минимизировать размер изображения до приемлемого качества. Это позволяет нам хранить больше изображений в том же пространстве, что и раньше.
Мы используем разложение по сингулярным значениям при обработке изображений, чтобы сократить трудоемкость задач. Это использует тот факт, что несколько сингулярных значений, полученных после SVD, являются большими. Мы можем обрезать три матрицы в соответствии с первыми несколькими сингулярными значениями и получить сжатое приближение исходного изображения.
SVD для удаления фона из видео
Мы часто задумываемся о роскошном и крутом прошлом актеров в рекламных роликах и программах. Многие делают это вручную, но некоторые выбирают машинное обучение, чтобы избежать ручного труда. Поскольку фон видео статичен и не имеет большого движения, чего нельзя сказать о переднем плане, мы можем использовать эту функцию для разделения фона и переднего плана с помощью SVD.








