A * Алгоритм в AI: концепции и реализация

Алгоритмы поиска предназначены для поиска или извлечения элементов из структуры данных, где они хранятся. Они необходимы для доступа к желаемым элементам в структуре данных и извлечения их при необходимости. Важным аспектом поисковых алгоритмов является нахождение пути, который используется для нахождения путей, по которым можно перемещаться из одной точки в другую, путем нахождения наиболее оптимального маршрута.

В этом руководстве по алгоритму A * вы узнаете об алгоритме A *, алгоритме поиска, который находит кратчайший путь между двумя точками.

Что такое алгоритм A *?

Это алгоритм поиска, используемый для нахождения кратчайшего пути между начальной и конечной точками. 
Он часто используется для обхода карты с целью нахождения кратчайшего пути. 
A * изначально был разработан как задача обхода графа, чтобы помочь построить робота, который может находить свой собственный курс. 
Он остается широко популярным алгоритмом обхода графа.

Сначала он ищет более короткие пути, что делает его оптимальным и полным алгоритмом. Оптимальный алгоритм найдет результат с наименьшими затратами для решения проблемы, в то время как полный алгоритм найдет все возможные результаты решения проблемы.

Еще одним аспектом, который делает A * таким мощным, является реализация взвешенных графиков. Взвешенный график использует числа для представления стоимости прохождения каждого пути или курса действий. Это означает, что алгоритмы могут выбрать путь с наименьшими затратами и найти наилучший маршрут с точки зрения расстояния и времени.

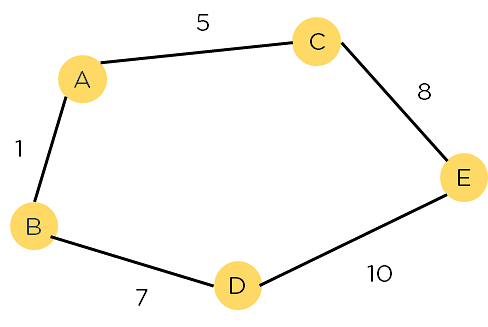
Рисунок 1: взвешенный график

Основным недостатком алгоритма является его пространственная и временная сложность. Требуется много места для хранения всех возможных путей и много времени для их поиска.

Приложения алгоритма A *

Алгоритм A * широко используется в различных областях для поиска путей и задач оптимизации. Он находит применение в робототехнике, видеоиграх, планировании маршрутов, логистике и искусственном интеллекте. В робототехнике A * помогает роботам преодолевать препятствия и находить оптимальные пути. В видеоиграх он позволяет неигровым персонажам разумно ориентироваться в игровом окружении. Приложения для планирования маршрутов используют A * для поиска кратчайших маршрутов между локациями. Отрасли логистики используют A * для маршрутизации транспортных средств и составления расписания. A * также используется в системах искусственного интеллекта, таких как обработка естественного языка и машинное обучение, для оптимизации процессов принятия решений. Его универсальность и эффективность делают его ценным алгоритмом во многих реальных сценариях.

Почему алгоритм поиска A *?

Алгоритм поиска A * – это простой и эффективный алгоритм поиска, который можно использовать для нахождения оптимального пути между двумя узлами графа. Он будет использоваться для нахождения кратчайшего пути. Это расширение алгоритма кратчайшего пути Дейкстры (Алгоритм Дейкстры). Расширение здесь заключается в том, что вместо использования приоритетной очереди для хранения всех элементов мы используем кучи (бинарные деревья) для их хранения. Алгоритм поиска A * также использует эвристическую функцию, которая предоставляет дополнительную информацию о том, как далеко мы находимся от целевого узла. Эта функция используется в сочетании со структурой данных f-heap, чтобы сделать поиск более эффективным.

Давайте теперь рассмотрим краткое объяснение алгоритма A *.

Объяснение

В том случае, если у нас есть сетка с большим количеством препятствий и мы хотим добраться куда-то как можно быстрее, алгоритмы поиска A * – наш спаситель. Из заданной начальной ячейки мы можем добраться до целевой ячейки как можно быстрее. Сумма значений двух переменных определяет узел, который она выбирает в любой момент времени.

На каждом шаге он выбирает узел с наименьшим значением ‘f’ (сумма ‘g’ и ‘h’) и обрабатывает этот узел / ячейку. ‘g’ и ‘h’ определяются как можно проще ниже:

• ‘g’ – это расстояние, необходимое, чтобы добраться до определенного квадрата на сетке от начальной точки, следуя пути, который мы сгенерировали, чтобы добраться туда.
• ‘h’ – это эвристика, представляющая собой оценку расстояния, необходимого для того, чтобы добраться до финиша из этого квадрата сетки.

Эвристика – это, по сути, обоснованные догадки. Важно понимать, что мы не знаем расстояния до конечной точки, пока не найдем маршрут, поскольку существует очень много вещей, которые могут помешать (например, стены, вода и т.д.). В следующих разделах мы углубимся в то, как вычислять эвристику.

Давайте теперь рассмотрим подробный алгоритм A *.

Алгоритм

Начальное условие – мы создаем два списка – Открытый список и Закрытый список.

Теперь необходимо выполнить следующие шаги –

• Открытый список должен быть инициализирован.
• Поместите начальный узел в открытый список (оставьте его f равным нулю). Инициализируйте закрытый список.
• Следуйте инструкциям, пока открытый список не станет непустым:

1. Найдите узел с наименьшим значением f в открытом списке и назовите его “q”.
2. Удалить Q из открытого списка.
3. Создайте восемь потомков q и установите q в качестве их родительского элемента.
4. Для каждого потомка:

i) Если целью является поиск преемника, прекратите поиски

ii) В противном случае вычислите g и h для преемника.

преемник.g = q.g + вычисленное расстояние между преемником и q .

преемник.h = вычисленное расстояние между преемником и целью. Для этого мы рассмотрим три эвристики: диагональную, евклидову и эвристику Манхэттена.

преемник.f = преемник.g плюс преемник.h

iii) Пропустите этого преемника, если в ОТКРЫТОМ списке присутствует узел с тем же местоположением, что и у него, но значение f ниже, чем у преемника.

iv) Пропустите преемника, если в ЗАКРЫТОМ списке есть узел с той же позицией, что и у преемника, но меньшим значением f; в противном случае добавьте узел в конец открытого списка (цикл for).

• Поместите Q в закрытый список и завершите цикл while.

Теперь мы обсудим, как рассчитать эвристику для узлов.

Эвристика

Мы можем легко вычислить g, но как нам вычислить h?

Есть два метода, которые мы можем использовать для вычисления значения h:

1. Определите точное значение h (что, безусловно, отнимает много времени).

(или)

2. Используйте различные методы для аппроксимации значения h. (менее трудоемко).

Давайте обсудим оба метода.

Точная эвристика

Хотя мы можем получить точные значения h, обычно это занимает очень много времени.

Способы определения точного значения h перечислены ниже.

1. Перед использованием алгоритма поиска A * предварительно вычислите расстояние между каждой парой ячеек.

2. Используя формулу расстояния / евклидово расстояние, мы можем напрямую определить точное значение h при отсутствии заблокированных ячеек или препятствий.

Давайте посмотрим, как вычислить эвристику аппроксимации.

Эвристика аппроксимации

Для определения h обычно используются три эвристики аппроксимации:

1. Расстояние до Манхэттена

Расстояние Манхэттена – это сумма абсолютных значений расхождений между координатами x и y текущей и целевой ячеек.

Формула вкратце приведена ниже –

h = abs (curr_cell.x – goal.x) +

abs (curr_cell.y – цель.y)

Мы должны использовать этот эвристический метод, когда нам разрешено двигаться только в четырех направлениях – сверху, влево, вправо и снизу.

Давайте теперь взглянем на метод диагонального расстояния, чтобы вычислить эвристику.

2. Расстояние по диагонали

Это не что иное, как наибольшее абсолютное значение разности между координатами x и y текущей ячейки и целевой ячейки.

Это суммируется ниже в следующей формуле –

dx = abs(curr_cell.x – goal.x)

dy = abs(curr_cell.y – цель.y)

h = D * (dx + dy) + (D2 – 2 * D) * min (dx, dy)

где D – длина каждого узла (по умолчанию = 1), а D2 – диагональ

Мы используем этот эвристический метод, когда нам разрешено двигаться только в восьми направлениях, подобно ходам короля в шахматах.

Давайте теперь взглянем на метод евклидова расстояния для вычисления эвристики.

3. Евклидово расстояние

Евклидово расстояние – это расстояние между целевой ячейкой и текущей ячейкой с использованием формулы расстояния:

h = sqrt ( (curr_cell.x – goal.x)^ 2 +

(curr_cell.y – цель.y)^ 2 )

Мы используем этот эвристический метод, когда нам разрешено двигаться в любом направлении по нашему выбору.

Ваша карьера в AI / ML не за горами!

Основная концепция алгоритма A *

Эвристический алгоритм жертвует оптимальностью, точностью и аккуратностью ради скорости, чтобы решать задачи быстрее и эффективнее.

Все графики имеют разные узлы или точки, которые алгоритм должен пройти, чтобы достичь конечного узла. Все пути между этими узлами имеют числовое значение, которое рассматривается как вес пути. Сумма всех поперечных путей дает вам стоимость этого маршрута.

Первоначально алгоритм вычисляет стоимость для всех своих ближайших соседних узлов, n, и выбирает тот, который требует наименьших затрат. Этот процесс повторяется до тех пор, пока новые узлы не будут выбраны и все пути не будут пройдены. Затем вам следует рассмотреть наилучший путь среди них. Если f (n) представляет конечную стоимость, то ее можно обозначить как :

f(n) = g(n) + h(n), где :

g (n) = стоимость перехода от одного узла к другому. Это будет варьироваться от узла к узлу

h (n) = эвристическая аппроксимация значения узла. Это не реальное значение, а стоимость аппроксимации

Как работает алгоритм A *?

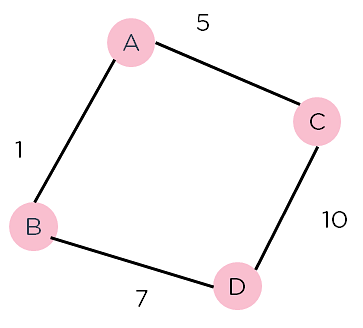
Рисунок 2: взвешенный график 2

Рассмотрим приведенный выше взвешенный график, который содержит узлы и расстояние между ними. Допустим, вы начинаете с A и должны перейти к D.

Теперь, поскольку начало находится в источнике A, который будет иметь некоторое начальное эвристическое значение. Следовательно, результаты следующие

f(A) = g(A) + h(A)
f(A) = 0 + 6 = 6

Далее проследите путь к другим соседним вершинам :

f (A-B) = 1 + 4

f (A-C) = 5 + 2

Теперь возьмите путь к месту назначения от этих узлов и вычислите веса :

f (A-B-D) = (1 + 7) + 0

f (A-C-D) = (5 + 10) + 0

Ясно, что узел B указывает вам наилучший путь, так что именно по этому узлу вам нужно пройти, чтобы добраться до места назначения.

Псевдокод алгоритма A *

Приведенный ниже текст представляет собой псевдокод алгоритма. Он может быть использован для реализации алгоритма на любом языке программирования и является базовой логикой, лежащей в основе алгоритма.

• Создайте открытый список, содержащий начальный узел
  • Если он достигнет конечного узла :
  • Создайте закрытый пустой список
  • Если он не достигает узла назначения, тогда рассмотрите узел с наименьшим f-баллом в открытом списке

Мы закончили

• Ещё :

Поместите текущий узел в список и проверьте его соседей

• Для каждого соседа текущего узла :
  • Если сосед имеет меньшее значение g, чем текущий узел, и находится в закрытом списке:

Замените соседа этим новым узлом в качестве родительского соседа

• Еще, если (текущее значение g ниже, а соседний находится в открытом списке):

Замените соседа на меньшее значение g и измените родительский узел соседа на текущий узел.

• Еще, если соседа нет в обоих списках:

Добавьте его в открытый список и установите его g

Как реализовать алгоритм A *

1. Как реализовать алгоритм A * в Python

Рассмотрим график, показанный ниже. Узлы представлены розовыми кружочками, и приведены веса путей вдоль узлов. Числа над узлами представляют эвристическую ценность узлов.

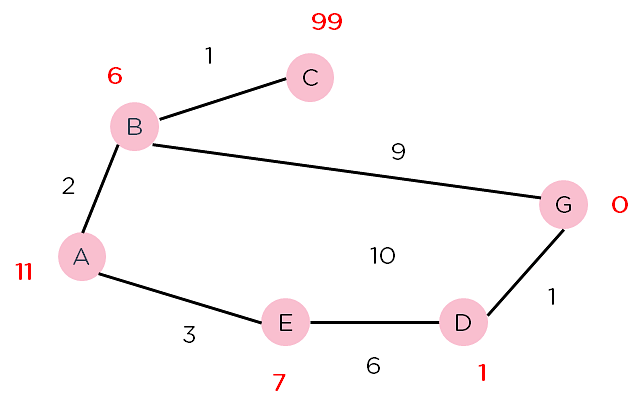
Рисунок 3: Взвешенный график для алгоритма A*

Вы начинаете с создания класса для алгоритма. Теперь опишите открытые и закрытые списки. Здесь вы используете наборы и два словаря – один для хранения расстояния от начального узла, а другой для родительских узлов. И инициализируйте их равными 0 и начальному узлу.

Рисунок 4: Инициализация важных параметров

Теперь найдите соседний узел с наименьшим значением f(n). Вы также должны закодировать условие достижения узла назначения. Если это не так, поместите текущий узел в открытый список, если его еще нет в нем, и установите его родительские узлы.

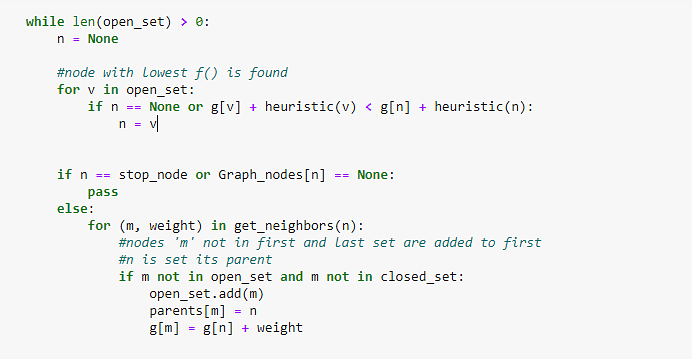
Рисунок 5: Добавление узлов в список открытых и настройка родительских узлов

Если соседний узел имеет меньшее значение g, чем текущий узел, и находится в закрытом списке, замените его этим новым узлом в качестве родительского узла соседа.

Рисунок 6: Проверка расстояний и обновление значений g

Если текущее значение g ниже предыдущего, а его сосед находится в открытом списке, замените его на меньшее значение g и измените родительское значение соседа на текущий узел.

Если соседа нет в обоих списках, добавьте его в открытый список и установите для него значение g.

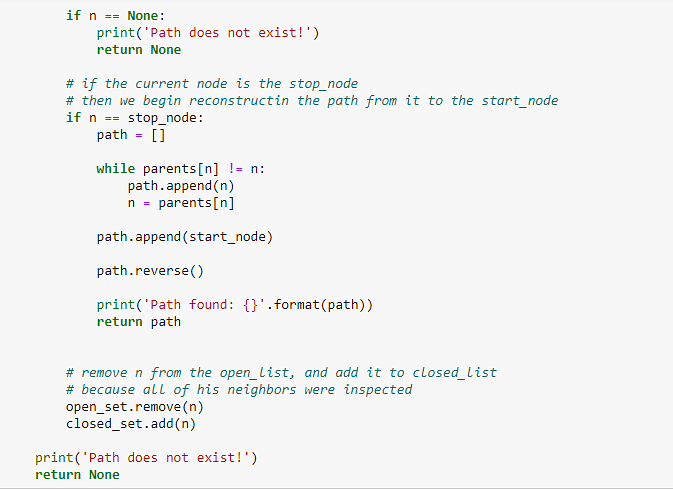
Рисунок 7: Проверка расстояний, обновление значений g и добавление родительских элементов

Теперь определите функцию для возврата соседей и их расстояний.

Рисунок 8: Определение соседей

Также создайте функцию для проверки эвристических значений.

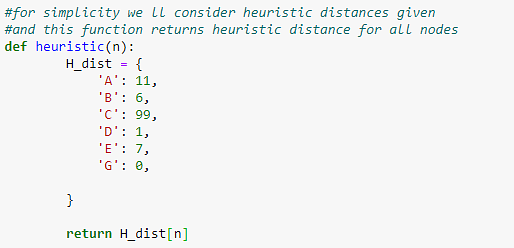
Рисунок 9: Определение функции для возврата эвристических значений

Давайте опишем наш график и вызовем функцию A star .

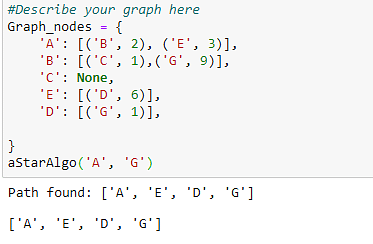
Рисунок 10: Вызов функции A*

Алгоритм проходит по графику и находит путь с наименьшими затратами

который выполняется через E => D => G.

2. Как реализовать алгоритм A * на C ++

#include <iostream>
#include <vector>
#include <queue>
#include <unordered_map>
#include <cmath>

struct Node {
    int x, y;
    float g, h;
    Node* parent;

    Node(int x, int y, float g, float h, Node* parent = nullptr)
        : x(x), y(y), g(g), h(h), parent(parent) {}

    float f() const { return g + h; }

    bool operator<(const Node& other) const {
        return f() > other.f();
    }
};

float heuristic(int x1, int y1, int x2, int y2) {
    return std::sqrt((x2 - x1) * (x2 - x1) + (y2 - y1) * (y2 - y1));
}

std::vector<Node> get_neighbors(const Node& node, const std::vector<std::vector<int>>& grid) {
    std::vector<Node> neighbors;
    std::vector<std::pair<int, int>> directions = {{1, 0}, {0, 1}, {-1, 0}, {0, -1}};

    for (auto& dir : directions) {
        int newX = node.x + dir.first;
        int newY = node.y + dir.second;
        if (newX >= 0 && newX < grid.size() && newY >= 0 && newY < grid[0].size() && grid[newX][newY] == 0) {
            neighbors.emplace_back(newX, newY, node.g + 1, 0, nullptr);
        }
    }
    return neighbors;
}

void reconstruct_path(Node* node) {
    while (node) {
        std::cout << "(" << node->x << "," << node->y << ") ";
        node = node->parent;
    }
    std::cout << std::endl;
}

void astar(const std::vector<std::vector<int>>& grid, int startX, int startY, int goalX, int goalY) {
    std::priority_queue<Node> openList;
    std::unordered_map<int, std::unordered_map<int, Node*>> allNodes;

    Node* startNode = new Node(startX, startY, 0, heuristic(startX, startY, goalX, goalY));
    openList.push(*startNode);
    allNodes[startX][startY] = startNode;

    while (!openList.empty()) {
        Node current = openList.top();
        openList.pop();

        if (current.x == goalX && current.y == goalY) {
            reconstruct_path(&current);
            return;
        }

        auto neighbors = get_neighbors(current, grid);
        for (auto& neighbor : neighbors) {
            neighbor.h = heuristic(neighbor.x, neighbor.y, goalX, goalY);
            neighbor.parent = allNodes[current.x][current.y];

            if (!allNodes[neighbor.x][neighbor.y] || neighbor.g < allNodes[neighbor.x][neighbor.y]->g) {
                allNodes[neighbor.x][neighbor.y] = new Node(neighbor);
                openList.push(neighbor);
            }
        }
    }

    std::cout << "No path found" << std::endl;
}

3. Как реализовать алгоритм A * в Java

import java.util.*;

class Node implements Comparable<Node> {
    int x, y;
    double g, h;
    Node parent;

    Node(int x, int y, double g, double h, Node parent) {
        this.x = x;
        this.y = y;
        this.g = g;
        this.h = h;
        this.parent = parent;
    }

    double f() {
        return g + h;
    }

    @Override
    public int compareTo(Node other) {
        return Double.compare(this.f(), other.f());
    }
}

public class AStar {
    static double heuristic(int x1, int y1, int x2, int y2) {
        return Math.sqrt(Math.pow(x2 - x1, 2) + Math.pow(y2 - y1, 2));
    }

    static List<Node> getNeighbors(Node node, int[][] grid) {
        List<Node> neighbors = new ArrayList<>();
        int[][] directions = {{1, 0}, {0, 1}, {-1, 0}, {0, -1}};

        for (int[] dir : directions) {
            int newX = node.x + dir[0];
            int newY = node.y + dir[1];
            if (newX >= 0 && newX < grid.length && newY >= 0 && newY < grid[0].length && grid[newX][newY] == 0) {
                neighbors.add(new Node(newX, newY, node.g + 1, 0, null));
            }
        }
        return neighbors;
    }

    static void reconstructPath(Node node) {
        while (node != null) {
            System.out.print("(" + node.x + "," + node.y + ") ");
            node = node.parent;
        }
        System.out.println();
    }

    static void astar(int[][] grid, int startX, int startY, int goalX, int goalY) {
        PriorityQueue<Node> openList = new PriorityQueue<>();
        Map<String, Node> allNodes = new HashMap<>();

        Node startNode = new Node(startX, startY, 0, heuristic(startX, startY, goalX, goalY), null);
        openList.add(startNode);
        allNodes.put(startX + "," + startY, startNode);

        while (!openList.isEmpty()) {
            Node current = openList.poll();

            if (current.x == goalX && current.y == goalY) {
                reconstructPath(current);
                return;
            }

            for (Node neighbor : getNeighbors(current, grid)) {
                neighbor.h = heuristic(neighbor.x, neighbor.y, goalX, goalY);
                neighbor.parent = current;

                String key = neighbor.x + "," + neighbor.y;
                if (!allNodes.containsKey(key) || neighbor.g < allNodes.get(key).g) {
                    allNodes.put(key, neighbor);
                    openList.add(neighbor);
                }
            }
        }

        System.out.println("No path found");
    }
}

4. Как реализовать алгоритм A * на C#

using System;
using System.Collections.Generic;

class Node : IComparable<Node> {
    public int x, y;
    public float g, h;
    public Node parent;

    public Node(int x, int y, float g, float h, Node parent = null) {
        this.x = x;
        this.y = y;
        this.g = g;
        this.h = h;
        this.parent = parent;
    }

    public float F() {
        return g + h;
    }

    public int CompareTo(Node other) {
        return F().CompareTo(other.F());
    }
}

class AStar {
    static float Heuristic(int x1, int y1, int x2, int y2) {
        return (float)Math.Sqrt(Math.Pow(x2 - x1, 2) + Math.Pow(y2 - y1, 2));
    }

    static List<Node> GetNeighbors(Node node, int[,] grid) {
        List<Node> neighbors = new List<Node>();
        int[,] directions = { { 1, 0 }, { 0, 1 }, { -1, 0 }, { 0, -1 } };

        for (int i = 0; i < directions.GetLength(0); i++) {
            int newX = node.x + directions[i, 0];
            int newY = node.y + directions[i, 1];
            if (newX >= 0 && newX < grid.GetLength(0) && newY >= 0 && newY < grid.GetLength(1) && grid[newX, newY] == 0) {
                neighbors.Add(new Node(newX, newY, node.g + 1, 0, null));
            }
        }
        return neighbors;
    }

    static void ReconstructPath(Node node) {
        while (node != null) {
            Console.Write($"({node.x},{node.y}) ");
            node = node.parent;
        }
        Console.WriteLine();
    }

    public static void AStarSearch(int[,] grid, int startX, int startY, int goalX, int goalY) {
        PriorityQueue<Node> openList = new PriorityQueue<Node>();
        Dictionary<string, Node> allNodes = new Dictionary<string, Node>();

        Node startNode = new Node(startX, startY, 0, Heuristic(startX, startY, goalX, goalY));
        openList.Enqueue(startNode);
        allNodes.Add($"{startX},{startY}", startNode);

        while (openList.Count > 0) {
            Node current = openList.Dequeue();

            if (current.x == goalX && current.y == goalY) {
                ReconstructPath(current);
                return;
            }

            foreach (Node neighbor in GetNeighbors(current, grid)) {
                neighbor.h = Heuristic(neighbor.x, neighbor.y, goalX, goalY);
                neighbor.parent = current;

                string key = $"{neighbor.x},{neighbor.y}";
                if (!allNodes.ContainsKey(key) || neighbor.g < allNodes[key].g) {
                    allNodes[key] = neighbor;
                    openList.Enqueue(neighbor);
                }
            }
        }

        Console.WriteLine("No path found");
    }
}

5. Как реализовать алгоритм A * в JavaScript

class Node {
    constructor(x, y, g, h, parent = null) {
        this.x = x;
        this.y = y;
        this.g = g;
        this.h = h;
        this.parent = parent;
    }

    f() {
        return this.g + this.h;
    }
}

function heuristic(x1, y1, x2, y2) {
    return Math.sqrt(Math.pow(x2 - x1, 2) + Math.pow(y2 - y1, 2));
}

function getNeighbors(node, grid) {
    const neighbors = [];
    const directions = [[1, 0], [0, 1], [-1, 0], [0, -1]];

    for (const [dx, dy] of directions) {
        const newX = node.x + dx;
        const newY = node.y + dy;
        if (newX >= 0 && newX < grid.length && newY >= 0 && newY < grid[0].length && grid[newX][newY] === 0) {
            neighbors.push(new Node(newX, newY, node.g + 1, 0, null));
        }
    }
    return neighbors;
}

function reconstructPath(node) {
    while (node) {
        console.log(`(${node.x},${node.y})`);
        node = node.parent;
    }
}

function astar(grid, startX, startY, goalX, goalY) {
    const openList = [];
    const allNodes = new Map();

    const startNode = new Node(startX, startY, 0, heuristic(startX, startY, goalX, goalY));
    openList.push(startNode);
    allNodes.set(`${startX},${startY}`, startNode);

    while (openList.length > 0) {
        openList.sort((a, b) => a.f() - b.f());
        const current = openList.shift();

        if (current.x === goalX && current.y === goalY) {
            reconstructPath(current);
            return;
        }

        const neighbors = getNeighbors(current, grid);
        for (const neighbor of neighbors) {
            neighbor.h = heuristic(neighbor.x, neighbor.y, goalX, goalY);
            neighbor.parent = current;

            const key = `${neighbor.x},${neighbor.y}`;
            if (!allNodes.has(key) || neighbor.g < allNodes.get(key).g) {
                allNodes.set(key, neighbor);
                openList.push(neighbor);
            }
        }
    }

    console.log("No path found");
}

Эти реализации являются базовыми и предполагают карту на основе сетки, где 0 представляет ячейку, по которой можно пройти, а любое другое значение представляет препятствие. Алгоритм A * использует приоритетную очередь (или аналогичную структуру) для первого исследования узлов с наименьшими затратами. Используемая эвристика – это евклидово расстояние, но в зависимости от задачи могут быть применены и другие эвристики, такие как расстояние Манхэттена.

Обязательно скорректируйте эти реализации в соответствии с конкретными потребностями вашего приложения, например, добавьте более сложную обработку препятствий, реализуйте очередь с лучшим приоритетом или улучшите реконструкцию пути.

Преимущества алгоритма A * в AI

Алгоритм A * обладает рядом преимуществ.

• Во-первых, он гарантирует нахождение оптимального пути при использовании соответствующей эвристики.
• Во-вторых, он эффективен и может обрабатывать большие пространства поиска, эффективно сокращая бесперспективные пути.
• В-третьих, его можно легко адаптировать к различным проблемным областям и эвристикам.
• В-четвертых, A * является гибким и может быть адаптирован к различным затратам на местности или ограничениям. Кроме того, он широко реализован и располагает огромным количеством доступных ресурсов и поддержки.

В целом, преимущества алгоритма A * в AI делают его популярным выбором для решения задач поиска путей и оптимизации.

Недостатки алгоритма A * в AI

Хотя алгоритм A * в AI имеет множество преимуществ, он также имеет некоторые ограничения.

• Одним из недостатков является то, что A * может быть дорогостоящим с точки зрения вычислений в определенных сценариях, особенно когда пространство поиска обширно и количество возможных путей велико.
• Алгоритм может потреблять значительные ресурсы памяти и обработки.
• Другое ограничение заключается в том, что A * в значительной степени зависит от качества эвристической функции. Если эвристика плохо разработана или неточно оценивает расстояние до цели, производительность и оптимальность алгоритма могут быть поставлены под угрозу.
• Кроме того, A * может иметь проблемы с определенными типами графиков или пространствами поиска, которые демонстрируют нерегулярные или непредсказуемые структуры.

Что, если пространство поиска в алгоритме A * представляет собой не сетку, а график?

Алгоритм A * может применяться к пространствам поиска без сетки, которые представлены в виде графиков. В этом случае узлы графика представляют состояния или местоположения, а ребра представляют соединения или переходы между ними. Ключевое отличие заключается в определении соседей для каждого узла, которое определяется ребрами на графике, а не соседними ячейками в сетке. Алгоритм A * по-прежнему можно использовать для нахождения оптимального пути в таких пространствах поиска на основе графов путем соответствующего определения эвристической функции и реализации необходимых структур данных и алгоритмов для обхода графа.

A * Пример алгоритма

A * был успешно применен во многих реальных сценариях. Например, при планировании траектории движения роботов A * помогает роботам ориентироваться в динамичной среде, избегая препятствий. При разработке игр A * используется для создания интеллектуального искусственного интеллекта противника, который может эффективно преследовать игрока. В логистике и транспортировке A * помогает находить оптимальные маршруты для транспортных средств доставки, минимизируя время и затраты. Кроме того, алгоритм A * находит применение в сетевой маршрутизации, например, для поиска кратчайшего пути в компьютерной сети. Эти примеры подчеркивают универсальность и практичность концепций и реализаций алгоритма A * в различных областях.